Functional Programming with R

class: title-slide, left, bottom

# Functional Programming with R
----
## **NHS-R Conference 2021**
### **[Tom Jemmett][email]** | Senior Healthcare Analyst
### **[The Strategy Unit][su]** | Midlands and Lancashire CSU

---

# Session Outline

* What are functions?
* Why do we want to write functions?
* What is functional programming?
* A run through of the `{purrr}` package
  - `compose` and `partial`
  - `map` and it's variants
  - `reduce`
  - `safely` and `possibly`
  - `keep` and `discard`
  - `some`/`every`/`none`
* A brief introduction to Parallel Computation with `{furrr}`

---

# About The Strategy Unit / Me

.pull-left[
"Leading research, analysis and change from within the NHS"

The Strategy Unit is a specialist NHS team, based in Midlands and Lancashire Commissioning Support Unit. We focus on
the application of high-quality, multi-disciplinary analytical work.

Our team comes from diverse backgrounds. Our academic qualifications include maths, economics, history, natural
sciences, medicine, sociology, business and management, psychology and political science. Our career and personal
histories are just as varied.

Our staff are NHS employees, animated by NHS values. The Strategy Unit covers all its costs through project funding.
But this is driven by need, not what we can sell. Any surplus is recycled for public benefit.

[strategyunitwm.nhs.uk](https://strategyunitwm.nhs.uk/)/[GitHub](https://github.com/The-Strategy-Unit)
]

.pull-right[
**Tom Jemmett**

*Senior Healthcare Analyst*

[thomas.jemmett@nhs.net](mailto:thomas.jemmett@nhs.net)

- 10+ years experience within the NHS as a data analyst
- BSc Computer Science and Pure Mathematics (Open University)
- MBCS/AMIMA
- Active member of NHS-R community
- Senior Fellow of NHS-R academy
- @tomjemmett [Twitter](https://twitter.com/tomjemmett)/[GitHub](https://github.com/tomjemmett)
]

---
class: middle, center

# What are functions?

---

## What are functions?

.pull-left[

A function is a process which takes some input, called **arguments**, and produces some output called a **return
value**. Functions may serve the following purposes:

* **Mapping**: Produce some output based on given inputs. A function **maps** input values to output values.

* **Procedures**: A function may be called to perform a sequence of steps. The sequence is known as a procedure, and
programming in this style is known as **procedural programming**.

* **I/O**: Some functions exist to communicate with other parts of the system, such as the screen, storage, system logs
or network.

source: ["What is a pure function?"][mji_what_pure_fn]

]

.pull-right[

``` r
# mapping
fn <- function(x) {
  x * x + 1
}
```

``` r
# procedure
counter <- 0
stack <- list()

push <- function(x) {
  counter <<- counter + 1
  stack[[counter]] <<- x
}
```

``` r
# i/o:
read_csv(filename)
```
]

---

## Vectors in R

In R we have a number of different types of vectors:

* Atomic vectors of 1-dimension, e.g. `c(1, 2, 3)` and `c("hello", "world")`. All values in these vectors contain the
same type of data (they are **homogeneous**)
* Lists are vectors where each item can be an atomic vector, or another list. The items in a list need not be the same
type, nor do they have to be the same length (they are **heterogeneous**). E.g., we can have
``` r
list(
  c(1, 2, 3),
  c("hello", "world"),
  list('a', 'b')
)
```
* Items in atomic vectors or lists can be named, e.g. `c('a' = 1, 'b' = 2)`.
* Dataframes are just special cases of lists: each item in the list must have the same length. Each item is a column,
and the name of the item is the name of the column. That is, `length(df) == ncol(df)`.
* Matrices/Arrays are 2-d and n-d atomic vectors. We won't cover these today, but care needs to be taken when using
these as they can easily be coerced into a 1-d vector (e.g. with a matrix by running through all the items in the first
column, then all the items in the second column etc.)

---

## Environments

.pull-left[
In R, we have the global environment. This is where all variables are created when you assign (`<-`) something in the
console.

When a function is evaluated, it creates it's own environment. All of the arguments that are passed to the function,
along with any variables created in the function are stored in this new environment.

The function's environment's parent will be the global environment, so we can see all of the variables created in the
global environment. Variables that are created in the function's environment aren't visible from the global environment
though.

If we reassign a variable in a function it will take a copy of that variable rather than mutating the value in the
global environment. If we want to update `x` in the global environment we need to use the `<<-` operator.
]
.pull-right[

```r
x <- 1
fn <- function(y) {
  x <- x * 2
  z <- x + y
  z
}
result <- fn(2)
```

```r
exists("z")
```

```
## [1] FALSE
```

```r
x
```

```
## [1] 1
```
]

---

# Why do we want to write functions?

Consider the following code (from the book [R4DS][r4ds]). Can you spot the mistake?

``` r
df <- tibble::tibble(
  a = rnorm(10),
  b = rnorm(10),
  c = rnorm(10),
  d = rnorm(10)
)

df$a <- (df$a - min(df$a, na.rm = T)) / 
  (max(df$a, na.rm = T) - min(df$a, na.rm = T))
df$b <- (df$b - min(df$b, na.rm = T)) / 
  (max(df$b, na.rm = T) - min(df$a, na.rm = T))
df$c <- (df$c - min(df$c, na.rm = TRUE)) / 
  (max(df$c, na.rm = T) - min(df$c, na.rm = T))
df$d <- (df$d - min(df$d, na.rm = TRUE)) / 
  (max(df$d, na.rm = T) - min(df$d, na.rm = T))
```

---

## The mistake

``` r
df$b <- (df$b - min(df$b, na.rm = T)) / 
  (max(df$b, na.rm = T) - min(df$a, na.rm = T))
```

Often, when we copy and paste code we introduce subtle bugs, in the previous example we forgot to update the one
argument: me call `min(df$a)` rather than `min(df$b)`.

Writing functions can reduce these types of errors by abstracting away the underlying logic.

---

## Creating a function to solve the last problem

.pull-left[
To the right is one way to turn the previous example into a function.

We pass in a numerical vector (`x` to the function), calculate the minimum and maximum values, then rescale the vector.

Finally we update each column, one by one, using this new function.

We still have an issue here with the potential for copy-paste bugs in that we are doing the same thing 4 times, just
changing the column in the data frame that we are using.

We could use a loop, but we will see how functional programming can help us solve this problem more elegantly later.

One important principle functions help us achieve is **DRY** (don't repeat yourself).
]

.pull-right[
``` r
rescale_01 <- function(x) {
  min_x <- min(x, na.rm = TRUE)
  max_x <- max(x, na.rm = TRUE)
  
  (x - min_x) / (max_x - min_x)
}
```

``` r
# update the columns
df$a <- rescale_01(df$a)
df$b <- rescale_01(df$b)
df$c <- rescale_01(df$c)
df$d <- rescale_01(df$d)
```

``` r
# using a loop
for (i in colnames(df)) {
  df[[i]] <- rescale_01(df[[i]])
}
```
]

---

# What is functional programming?

> Functional programming (often abbreviated FP) is the process of building software by composing **pure functions**,
> avoiding **shared state**, **mutable data**, and **side-effects**. Functional programming is **declarative** rather
> than **imperative**, and application state flows through pure functions. Contrast with object oriented programming,
> where application state is usually shared and colocated with methods in objects.
>
> …
>
> Functional code tends to be more concise, more predictable, and easier to test than imperative or object oriented code
> but if you’re unfamiliar with it and the common patterns associated with it, functional code can also seem a lot
> more dense, and the related literature can be impenetrable to newcomers.

["What is functional programming?", Mastering the JavaScript interview][mji_what_fp]

---

## Declarative vs Imperative

.pull-left[
Imperative programming uses statements to change a programs state. It often looks like a series of steps. You are 
telling the computer what to do at each step.

``` r
# Correlation panel
panel.cor <- function(x, y){
  usr <- par("usr"); on.exit(par(usr))
  par(usr = c(0, 1, 0, 1))
  r <- round(cor(x, y), digits=2)
  txt <- paste0("R = ", r)
  cex.cor <- 0.8/strwidth(txt)
  text(0.5, 0.5, txt, cex = cex.cor * r)
}
# Customize upper panel
upper.panel<-function(x, y){
  points(x,y, pch = 19, col = my_cols[iris$Species])
}
# Create the plots
pairs(iris[,1:4], 
      lower.panel = panel.cor,
      upper.panel = upper.panel)
```

[Source](http://www.sthda.com/english/wiki/scatter-plot-matrices-r-base-graphs)
]
.pull-right[
In contrast, declarative programming focuses on what the program should do, rather than how to do it. Examples of
declarative programming languages include Sql; you do not care how to actually perform the query, you just instruct
the computer what things you want:

``` sql
SELECT
  things
FROM
  my_table
WHERE
  stuff = '...';
```
]

---

## Pure functions

.pull-left[
Pure functions are functions which:

* always produce the same result given the same input

* have no side effects (e.g. reading from a database, writing a file to disk)

* do not use global state (e.g. using variables declared outside of the function)

From before, mappings are pure functions, but the other two types are not.

Pure functions are analogous to mathematical functions.

]

.pull-right[

.panelset[
.panel[.panel-name[pure functions]
``` r
function(x, y) {
  x + y
}

function(y) {
  function(x) {
    x + y
  }
}
```
]
.panel[.panel-name[non-pure functions]
``` r
rnorm(10)
read_csv("file.csv")

function(x) {
  Sys.Date() + x
}

function(x) {
  x + y
}

function(x) {
  function() {
    x <<- x + 1
    x
  }
}
```
]
]

]

---

## Mathematical Functions

.pull-left[
In contrast to the definition of a function in programming, the definition of a function in mathematics is concrete. A
function
`$$f : A \rightarrow B$$`
is a relationship between two set's, `$A$` and `$B$`, such that every
element from `$A$` is mapped to exactly one element in `$B$`.

.center[.image-50[
![](https://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Function_color_example_3.svg/330px-Function_color_example_3.svg.png)
]]
]

.pull-right[

Given two functions,

`$$f: A \rightarrow B\qquad\textrm{and}\qquad g: B \rightarrow C$$`

we can create a new function

`$$H: A \rightarrow C$$`

By composing `$f$` and `$g$`, we write this as `$g \cdot f$` (g after f).

Composition is a powerful tool as it allows us to build complexity by chaining together (simpler) functions.

]

---
class: middle, center

# Why do we care about pure functions?

---

## Referential Transparency

.pull-left[
Pure functions are useful as they can make code significantly easier to debug and test. Pure functions have the property
of [referential transparency][ref_transp], which put simply means we can replace an expression with it's corresponding
value.

For example, consider the function `fn` (shown to the right). Because the function `fn` is pure, we know that it will
always return the same result given the same input, so replacing it's call with the return value is going to yield the
same result.

This can make debugging/testing `another_fn` simpler. The behaviour of `another_fn` is not dependent on `fn`.
]

.pull-right[
``` r
fn <- function(x) {
  x + 3
}
```

``` r
another_fn(fn(3), 2)
```

``` r
# we can replace the call to fn() with
# it's return value
another_fn(6, 2)
```
]

---

## Testing

.pull-left[
Knowing that a function will always return the same value given the same inputs makes writing unit tests for the
function significantly easier because:

* We don't need to set up the global environment correctly before running the function - functions that rely on global
state would need to test the function multiple times with the global environment set up with all the possible values.

* We don't need to check the side effects of the function, we just need to check the return value is as expected.
Functions that rely on a side effect can suffer transient errors, e.g. you try to read data from a database, but the
server is temporarily down/busy.

* All we need to do is check that the outputs are correct for given inputs.
]

.pull-right[
``` r
library(testthat)

triangle_number <- function(x) {
  0.5 * x * (x + 1)
}

test_that("it works as expected", {
  expected_that(triangle_number(1),  1)  
  expected_that(triangle_number(2),  3)  
  expected_that(triangle_number(3),  6)  
  expected_that(triangle_number(4), 10)  
  expected_that(triangle_number(5), 15)  
})
```
]

---

## Parallel Computation

.pull-left[

Writing parallisable code which relies on either shared state or side effect's is notoriously difficult.

Consider the following:

``` r
counter <- 0
increment <- function() {
  counter <<- counter + 1
}
```

If we tried to run this function twice in parallel, if both workers try to start at exactly the same time they will both
see `counter` as 0. So both will try to set `counter` to 1, not 2 as may be expected.

That is, we depend on the order of evaluation, and the timing of when they functions are called.
]

.pull-right[
Pure functions however are easy to parallise, because if a function only depends on the arguments that it is provided
then this issue goes away.

The function calls never interact with each other, and can be evaluated in any order, we will always get the same
results as if we evaluated the calls one after another (up to order of results).

We will see later how the `{furrr}` package can help us to parallelise code.
]

---

# Higher order functions

.pull-left[
A higher order function is a function which either:

* takes a function as an argument,
* or, returns a function.

Functions in R are what we call "first class citizens": they are like any other value (such as a numeric vector, or a
character).

As such, we can simply pass a function as an argument just by using it's name, or we can return a function
by creating a function and using that as the return value.

For example, the following is valid code in R:

``` r
my_function <- function(fn, x) {
  force(x)
  return(function(y) fn(x, y))
}
```
]

.pull-right[
The example given to the left takes a function `fn` which expects two arguments, `x` and `y`, and returns a new function
which always uses the same value for the `x` argument.

This is called **partial application** and can be a very powerful tool in functional programming - we are making a new
function from existing functions.

The `{purrr}` package has a function just for this purpose:

```r
add_three <- purrr::partial(`+`, 3)
add_three(2)
```

```
## [1] 5
```
]

---

## Composition

.pull-left[
If we have 2 (or more) **pure** functions, and we know that the return type for one function is the input type for the next,
then we can build a new function that composes these functions together. `{purrr}` has a function that does this for us,
called `compose`.

``` r
f <- function(x) x * 2
g <- function(x) x + 3

4 %>% f() %>% g() # 11
5 %>% f() %>% g() # 13

h <- compose(g, f)
h(4) # 11
h(5) # 13
```

]

.pull-right[
The one downside to compose is if our functions accept multiple arguments.

To get around this we can combine `compose` and `partial`:

``` r
f <- function(x, y) x * y
g <- function(x, y) x + y

4 %>% f(2) %>% g(3) # 11
5 %>% f(3) %>% g(3) # 18

h <- compose(partial(g, y = 3), f)
h(4, 2) # 11
h(5, 3) # 18
```
]

In some respects, `compose` is like `%>%`: the difference is `compose` creates a new function which can be reused in
other parts of our code easily.

---

# Iteration with loops

.pull-left[
Previously we looked at an example where we used a for loop to run the same function on every column in a dataframe.

We had to iterate in this way because the function that we had (`rescale_01`) worked on individual numeric vectors.

We needed to set up the for loop by first extracting the list of columns, then iterating over each column running the
function.

This is a very common pattern: take a list we want to iterate over, then evaluate some function using that list.

``` r
for(i in colnames(df)) {
  df[[i]] <- rescale_01(df[[i]])
}
```
]

.pull-right[

However, it's very easy to make a mistake creating a loop this way: what if we occidentally update the wrong item in the
dataframe?

``` r
for(i in colnames(df)) {
  df[[1]] <- rescale_01(df[[i]])
}
```

Or we don't correctly initialise the iteration?

``` r
for(i in 1:4) {
  # does our data always have 4 columns?
  df[[i]] <- rescale_01(df[[i]])
}
```
]

---

# `purrr::map()`

.pull-left[
The `map` function from `{purrr}` takes a vector/list, and a function. It the evaluates the function once for each
input, returning the results as a list.

We could replace our loop example quite simply with a map function:

``` r
df <- map_dfc(df, rescale_01)
```

The map function's arguments are

``` r
map(x, fn, ...)
```

where

* `x` is the vector you wish to iterate over
* `fn` if the function
* ... are any extra arguments the function requires (these are the same for all calls of the function)
]

.pull-right[
The image, courtesy of [adv-r] shows graphically how the map function works.

![](https://d33wubrfki0l68.cloudfront.net/f0494d020aa517ae7b1011cea4c4a9f21702df8b/2577b/diagrams/functionals/map.png)
]

---

# `map` in action

.pull-left[
A toy example, let's take a vector of numbers and double them
``` r
values <- 1:5

# we can use a "named function"
double_num <- function(x) 2 * x
map(values, double_num)

# or, we can use an anonymous function
map(values, function(x) 2 * x)
# with R > 4.1, we can use \(x) 2 * x
map(values, \(x) 2 * x)

# we can also use a formula
map(values, ~ .x * 2)
```
]

.pull-right[
Any one of these would return the same thing: a list containing the results

```
## [[1]]
## [1] 2
## 
## [[2]]
## [1] 4
## 
## [[3]]
## [1] 6
## 
## [[4]]
## [1] 8
## 
## [[5]]
## [1] 10
```
]

---

# `map_*` variants

.pull-left[
In the previous example we can see the output of `map` is a list. It would be more useful for that function to return a
numeric vector instead. Fortunately, there is a simple way to achieve this in purrr:

```r
map_dbl(values, \(x) 2 * x)
```

```
## [1]  2  4  6  8 10
```

The variants provided are:

* `map_chr` for a function which returns a character
* `map_int`/`map_dbl` for a function which returns an integer/double
* `map_lgl` for a function which returns a logical (`TRUE`/`FALSE`)
* `map_raw` for a function which returns a raw
* `map_df`/`map_dfr`/`map_dfc` for a function which returns a dataframe

]

.pull-right[

There work so long as the function returns a single one of these values so
``` r
length(x) == length(map(x, fn))
```

Now, the example given so far isn't particularly useful: many operations in R are vectorised, so we could just do
`2 * values` and we would get exactly the same results as `map_dbl(values, \(x) 2 * x)`.

`map` functions are useful for cases where we have functions which aren't vectorised and we need to run the function
once for each item in the input vector.

]

---

# `map_df` variants

The data frame variants all do the same sort of thing: if a function returns a dataframe, rather than returning a list
of dataframes, it will bind the results together into a single dataframe:

* `map_df` and `map_dfr` use `bind_rows` to "union" the results together
* `map_dfc` uses `bind_cols` instead

One of the best use cases for `map_df` is to read in a folder full of csv's and combine the results together.

First, let's get a list of all the files in a folder. In this particular folder our files are named `YYYY-MM-DD.csv`.
The dir command with `full.names = TRUE` will return the full file path, but it will be useful to name each item just
after the date part. We use the `set_names()` function from `{purrr}` to achieve this, it accepts a list of items, and
then either a vector of names, or a function to transform the vector by.

```r
files <- dir("data/ae_attendances/", "*.csv", full.names = TRUE) %>%
  set_names(function(.x) stringr::str_extract(.x, "\\d{4}-\\d{2}-\\d{2}"))
files[1:2]
```

```
##                           2016-04-01                           2016-05-01 
## "data/ae_attendances/2016-04-01.csv" "data/ae_attendances/2016-05-01.csv"
```

---

## `map_df` variants (continued)

Now that we have our list of files to load, we can use the `read_csv` function to load each csv file. Here, we pass to
the `read_csv` function the column types used in the files, and we also set the `.id` argument of `map_dfr`. This will
create a column in the final dataframe containing the "name" of each item in the list, e.g. the date from the filename.

```r
ae_attendances <- map_dfr(files, read_csv, col_types = "ccddd", .id = "period")
head(ae_attendances, 8)
```

```
## # A tibble: 8 x 6
##   period     org_code type  attendances breaches admissions
##   <chr>      <chr>    <chr>       <dbl>    <dbl>      <dbl>
## 1 2016-04-01 RF4      1           18788     4082       4074
## 2 2016-04-01 RF4      2             561        5          0
## 3 2016-04-01 RF4      other        2685       17          0
## 4 2016-04-01 R1H      1           27396     5099       6424
## 5 2016-04-01 R1H      2             700        5          0
## 6 2016-04-01 R1H      other       10317      143          0
## 7 2016-04-01 AD913    other        3836        1          0
## 8 2016-04-01 RYX      other       17369        0          0
```

---

## Functional Programming in dplyr

.pull-left[
You may have noticed that the `period` column before was a character - it would be much more useful to convert this to a
date.

We could just write a mutate statement like

``` r
ae_attendances %>%
  mutate(period = as.Date(period))
```

But, there is a much neater way of writing this out: we can use the `across` function from dplyr to apply a function to
a column.

`across` takes a column specification (either a name of a column, or a function like `where(is.numeric)`, and then a
function to apply to the column(s).

]

.pull-right[

```r
ae_attendances <- ae_attendances %>%
  mutate(across(period, as.Date))
head(ae_attendances, 4)
```

```
## # A tibble: 4 x 6
##   period     org_code type  attendances breaches admissions
##   <date>     <chr>    <chr>       <dbl>    <dbl>      <dbl>
## 1 2016-04-01 RF4      1           18788     4082       4074
## 2 2016-04-01 RF4      2             561        5          0
## 3 2016-04-01 RF4      other        2685       17          0
## 4 2016-04-01 R1H      1           27396     5099       6424
```
]

---

# `map2` and `imap`

So far we have looked at cases where we have a single vector to iterate over, but what if we have two vectors, both of
the same length? We can use the `map2` family of functions! There is `map2` which is equivalent to `map`, and then all
of the same `map2_*` variants as we just saw for `map`.

```r
letters <- c("a", "b", "c")
times <- 1:3

map2_chr(letters, times, \(x, y) paste(rep(x, y), collapse = ""))
```

```
## [1] "a"   "bb"  "ccc"
```

related to `map2` is `imap`. This only accepts a single vector, like `map`, but it creates a second "index" argument. If
the vector is named, this "index" will be the name of the item, otherwise it will be the numerical position.

```r
imap_chr(letters, \(x, y) paste(rep(x, y), collapse = ""))
```

```
## [1] "a"   "bb"  "ccc"
```

---

# `pmap`

.pull-left[
While `map` works with a single vector, and `map2` works with 2 vectors, `pmap` is a generalised version that works on
any number of vectors. `pmap` also has all of the variants that we have seen before.

Below is a toy example showing how `pmap` works. First, we need to construct a list that contains all of the vectors.
Note, the vectors must all be the same length: we are in effect going to loop over the first item from each vector, then
the second, etc. We then create a function which has one argument per vector.

```r
values <- list(1:3, 4:6, 7:9)
pmap_dbl(values, \(x, y, z) x * y + z)
```

```
## [1] 11 18 27
```
]

.pull-right[
If we instead use a named vector, then it will match the named items in the list to the arguments in the function, for
example, see how we get very different results when wee name the items differently from the order that the arguments
appear in the function.

```r
values <- list(z = 1:3, y = 4:6, x = 7:9)
pmap_dbl(values, \(x, y, z) x * y + z)
```

```
## [1] 29 42 57
```
]

---

# `pmap` in action: individual plots

.pull-left[
Facetted plots in ggplot are great, but what if you ever want to create individual plots and save the files?

First, let's use the `ae_attendances` dataset from the `{NHSRdatasets}` package. This contains 36 months of data of
A&E performance figures, split by trust and department type.

Let's say that we want to create a plot of attendaces for each of the different department types, summarised for every
trust.

Let's create a tibble that contains one row per department type, with a column that contains a nested dataset of all of
the rows of data for that group.
]

.pull-right[

```r
library(NHSRdatasets)

ae_types <- ae_attendances %>%
  group_by(type, period) %>%
  summarise(across(attendances, sum),
            .groups = "drop_last") %>%
  nest()

ae_types
```

```
## # A tibble: 3 x 2
## # Groups:   type [3]
##   type  data             
##   <fct> <list>           
## 1 1     <tibble [36 x 2]>
## 2 2     <tibble [36 x 2]>
## 3 other <tibble [36 x 2]>
```
]

---

# `pmap` in action: individual plots (continued...)

.pull-left[
We can take a quick sneaky look at the data stored in the nested data column:

```r
ae_types$data[[1]]
```

```
## # A tibble: 36 x 2
##    period     attendances
##    <date>           <dbl>
##  1 2016-04-01     1214057
##  2 2016-05-01     1353206
##  3 2016-06-01     1282499
##  4 2016-07-01     1353477
##  5 2016-08-01     1254439
##  6 2016-09-01     1277578
##  7 2016-10-01     1317571
##  8 2016-11-01     1258205
##  9 2016-12-01     1277133
## 10 2017-01-01     1237177
## # ... with 26 more rows
```
]

.pull-right[
And we could build a function that will plot this data:

```r
ae_plot <- function(type, data) {
  ggplot(data, aes(period, attendances)) +
    geom_line() + geom_point() +
    labs(title = paste("Type:", type))
}
ae_plot(ae_types$type[[1]], ae_types$data[[1]])
```

![](nhs-r-conf_21-fp_workshop_files/figure-html/unnamed-chunk-17-1.png)
]

---

# `pmap` in action: individual plots (continued...)

We can now tie this together to create our plots:

```r
plots <- pmap(ae_types, ae_plot)
```

.center[.image-50[.panelset[
.panel[.panel-name[type 1]
![](nhs-r-conf_21-fp_workshop_files/figure-html/unnamed-chunk-19-1.png)
]
.panel[.panel-name[type 2]
![](nhs-r-conf_21-fp_workshop_files/figure-html/unnamed-chunk-20-1.png)
]
.panel[.panel-name[type other]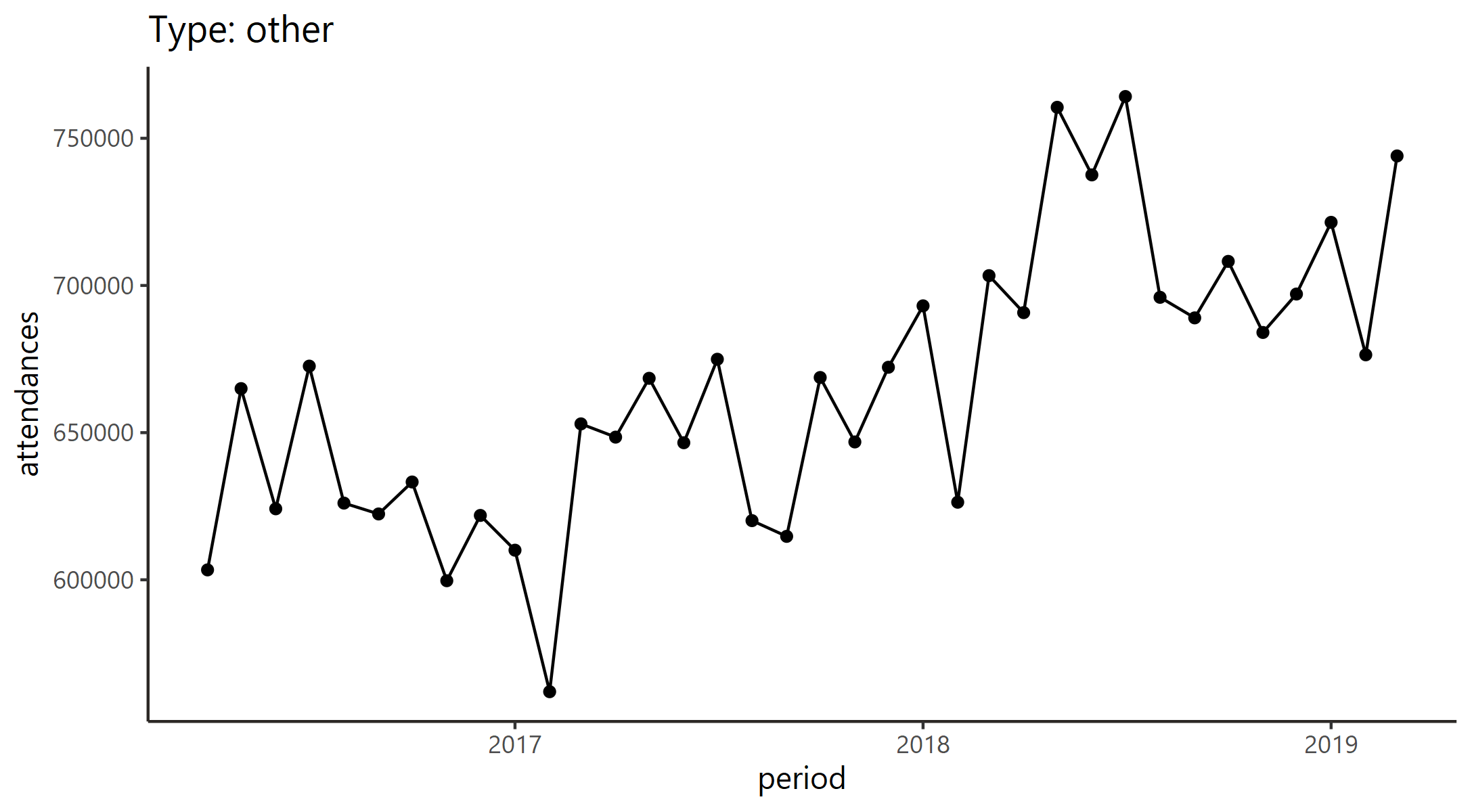
![](nhs-r-conf_21-fp_workshop_files/figure-html/unnamed-chunk-21-1.png)
]
]]]

---

# `walk`/`walk2`/`pwalk`

Along with `map`, `map2` and `pmap`, we have the `walk` family of functions: these are useful for if you want to run a
function for it's side-effect. For instance, in our previous example we created a list `plots` - what if we want to be
able to save these files to disk as `.png` files?

```r
walk2(paste0("plots/ae_plot_type_", ae_types$type, ".png"), plots, ggsave)
```

```
## Saving 7.25 x 4 in image
## Saving 7.25 x 4 in image
## Saving 7.25 x 4 in image
```

```r
dir("plots", pattern = ".png")
```

```
## [1] "ae_plot_type_1.png"     "ae_plot_type_2.png"     "ae_plot_type_other.png"
```

While functional programming tries to avoid side effects, sometimes they are very useful. In fact, without side effects
most programs wouldn't do a fat lot!

---

# `reduce`

.pull-left[
So far we've looked at iteration where we want to transform each item in a vector to a new thing. We end up with just as
many things as we started with. `reduce` is different in it's a way of successively combining our input vector into a
single value.

The image to the right (from [adv-r]) shows graphically how this works.

Here is a toy example, recreating the `sum` function by calling `+`.

```r
reduce(1:4, `+`)
```

```
## [1] 10
```

This is running `1 + 2` (3), then `3 + 3` (6), then `6 + 4` (10).
]

.pull-right[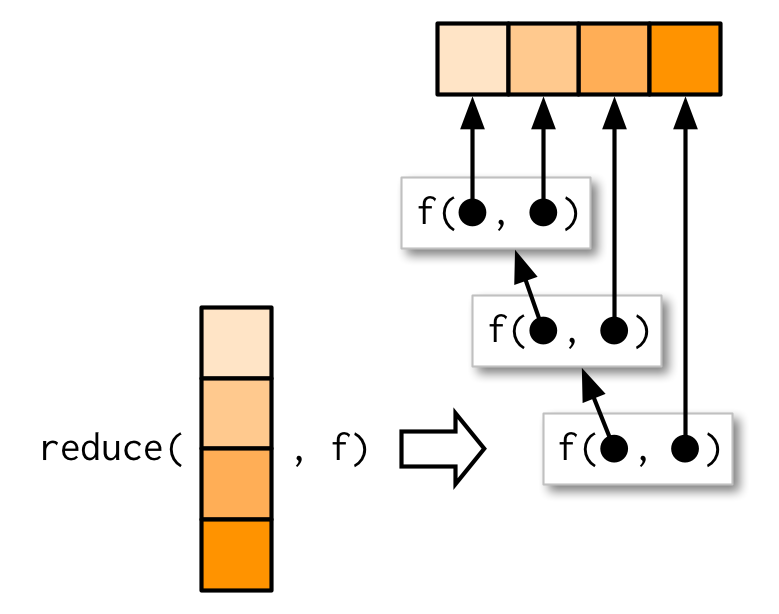
![](https://d33wubrfki0l68.cloudfront.net/9c239e1227c69b7a2c9c2df234c21f3e1c74dd57/eec0e/diagrams/functionals/reduce.png)
]

---

## When is `reduce` useful?

.pull-left[
In comparison to other programming languages, `reduce` is somewhat less useful in R due to so much of the language being
vectorised.

Where is is useful is if you have a function which works with two inputs (a binary function), but more than
two inputs. For example, what if we have a list of numbers, and we want to find the unique values that occur in every
list? (example borrowed from [adv-r]).

```r
numbers <- map(rep(15, 4),
               compose(sort, sample),
               x = 1:10, replace = TRUE)
str(numbers)
```

```
## List of 4
##  $ : int [1:15] 2 3 3 3 4 5 5 6 6 9 ...
##  $ : int [1:15] 1 3 3 4 5 7 7 7 8 9 ...
##  $ : int [1:15] 1 2 2 5 5 5 6 6 7 7 ...
##  $ : int [1:15] 1 1 2 2 4 4 5 6 6 6 ...
```
]

.pull-right[

The `intersect` function (from `{base}`) takes two vectors and returns a vector of the items which appear in both. We
can use this function with reduce to find our answer:

```r
reduce(numbers, intersect)
```

```
## [1]  5  9 10
```

]

---

# `reduce` arguments

By default, `reduce` will use the first item from the input as the "initial" value, but you can override this. This is
useful if you have a function which expects something of type `$A$` as the first argument, `$B$` as the second, and returns
an `$A$`.

For example, we could create a string of all of the sum of the numbers in our numeric vectors.

```r
reduce(numbers, \(x, y) paste(x, sum(y)), .init = "")
```

```
## [1] " 93 102 91 77"
```

We can also change the direction that reduce works in, by default it goes "forward" (e.g. it combines the first and
second items first, then the third...). We can change this with the `direction` argument (note how `x` and `y` have
flipped):

```r
reduce(numbers, \(x, y) paste(y, sum(x)), .init = "", .dir = "backward")
```

```
## [1] " 77 91 102 93"
```

---

# `safely`/`possibly`

.pull-left[
What happens if you have are mapping over some values, but an error happens?

```r
fn <- function(x) {
  if (x > 3) stop("too big!")
  x
}
try(map_dbl(1:4, fn))
```

```
## Error in .f(.x[[i]], ...) : too big!
```

Even though this function will work for some of the values, the whole thing errors! We can instead wrap our function in
either `safely` or `possibly` to handle these scenarios.
]

.pull-right[
.panelset[
.panel[.panel-name[possibly]

`possibly` wraps a function, and if the function errors it will instead return the value in the `otherwise` argument.

```r
map_dbl(1:4, possibly(fn, NA))
```

```
## [1]  1  2  3 NA
```
]

.panel[.panel-name[safely]

`safely` wraps a function and returns a list containing two items: `$result`, which is the value the function returns
(if an error occurs you will get NULL, unless you provide a value to `otherwise`), and `$error` which contains the error
message if the function errored.

```r
res <- map(1:4, safely(fn))
res[[4]]
```

```
## $result
## NULL
## 
## $error
## <simpleError in .f(...): too big!>
```
]

]
]

---

# `keep`/`discard`

`keep` and `discard` are very similar to the `filter` function in `{dplyr}`, except they work on vectors, not on
dataframes. For instance, let's say we want to filter a numeric vector based on some **predicate** function (a function
which returns a single `TRUE` or `FALSE` value).

.pull-left[

```r
is_even <- function(x) x %% 2 == 0

keep(1:5, is_even)
```

```
## [1] 2 4
```

```r
discard(1:5, is_even)
```

```
## [1] 1 3 5
```

]

.pull-right[

`{purrr}` has a number of functions for working with predicates, for instance, the `negate` function can be used to
give us the inverse of a predicate (as we can't write something like `!is_even`).

```r
keep(1:5, negate(is_even))
```

```
## [1] 1 3 5
```

]

---

# `some`/`every`/`none`

.pull-left[
In base R we have the functions `any` and `all`. These both take logical vectors and return either `TRUE` or `FALSE` if
any one of the values are `TRUE`, or all of the values are `TRUE` (respectively).

`{purrr}` provides the `some`, `every` and `none` functions which take vectors of any type, and a predicate function. It
then will run the predicate function on each item in the vector and return a single `TRUE` or `FALSE` value like `any`
and `all` do. `some` is the equivalent to `any`, `every` the equivalent to `all`, and `none` is the equivalent of not
`all`.

```r
values <- list(1:3, 4:6, 7:9)
map_dbl(values, sum)
```

```
## [1]  6 15 24
```
]

.pull-right[
.panelset[
.panel[.panel-name[A]

```r
sum_gt_5 <- \(x) sum(x) > 5

some(values, sum_gt_5)
```

```
## [1] TRUE
```

```r
every(values, sum_gt_5)
```

```
## [1] TRUE
```

```r
none(values, sum_gt_5)
```

```
## [1] FALSE
```
]

.panel[.panel-name[B]

```r
sum_gt_7 <- \(x) sum(x) > 7

some(values, sum_gt_7)
```

```
## [1] TRUE
```

```r
every(values, sum_gt_7)
```

```
## [1] FALSE
```

```r
none(values, sum_gt_7)
```

```
## [1] FALSE
```
]

.panel[.panel-name[C]

```r
sum_gt_25 <- \(x) sum(x) > 25

some(values, sum_gt_25)
```

```
## [1] FALSE
```

```r
every(values, sum_gt_25)
```

```
## [1] FALSE
```

```r
none(values, sum_gt_25)
```

```
## [1] TRUE
```
]
]
]

---

# Parallel Computation

The `{furrr}` package makes it easy to convert `map`'s to run in parallel. Almost all of the `map` functions are
available, prefixed with `future_`.

The first thing we need to do after loading the `{furrr}` package is set up the parallel workers. We do this with the
`plan` function.

.pull-left[

```r
library(furrr)
```

```
## Loading required package: future
```

```r
plan(multisession, workers = 10)
# multicore on Linux/Mac

fn <- function(x) {
  Sys.sleep(0.5)
  x
}
```
]

.pull-right[

```r
tictoc::tic()
x <- map_dbl(1:10, fn)
tictoc::toc()
```

```
## 5.13 sec elapsed
```

```r
tictoc::tic()
y <- future_map_dbl(1:10, fn)
tictoc::toc()
```

```
## 3.61 sec elapsed
```
]

---

# Further Reading / References

* [R4DS: Functions][r4ds]
* Advanced R
  - [Vectors](https://adv-r.hadley.nz/vectors-chap.html)
  - [Functions](https://adv-r.hadley.nz/functions.html)
  - [Environments](https://adv-r.hadley.nz/environments.html)
  - [Functional Programming][adv-r] (3 chapters)
* Mastering the javascript interview (while not R, the examples should be easy enough to follow)
  - [What is a pure function?][mji_what_pure_fn]
  - [What is functional Programming?][mji_what_fp]
* [Learn you a Haskell](http://learnyouahaskell.com/) (a purely functional programming language)
* Category Theory (the mathematics that underpins a lot of FP)
  - [B. Milewski Lectures](https://www.youtube.com/watch?v=I8LbkfSSR58&list=PLbgaMIhjbmEnaH_LTkxLI7FMa2HsnawM_)
  - [Category Theory for Programmers](https://bartoszmilewski.com/2014/10/28/category-theory-for-programmers-the-preface/)
  - [Category Theory Illustrated](https://boris-marinov.github.io/category-theory-illustrated/)
* [Lambda Calculus lecture](https://www.youtube.com/watch?v=6BnVo7EHO_8) (FP is derived from lambda calculus)

[//]: <> (URL's / References --------------------------------------------------)
[email]:mailto:thomas.jemmett@nhs.net
[su]:https://www.strategyunitwm.nhs.uk/
[mji_what_fp]: https://medium.com/javascript-scene/master-the-javascript-interview-what-is-functional-programming-7f218c68b3a0
[mji_what_pure_fn]: https://medium.com/javascript-scene/master-the-javascript-interview-what-is-a-pure-function-d1c076bec976
[ref_transp]: https://en.wikipedia.org/wiki/Referential_transparency
[r4ds]: https://r4ds.had.co.nz/functions.html
[adv-r]: https://adv-r.hadley.nz/functionals.html